Irregular functions and functional equations
Prof. Dr. H.-H. Kairies, TU Clausthal
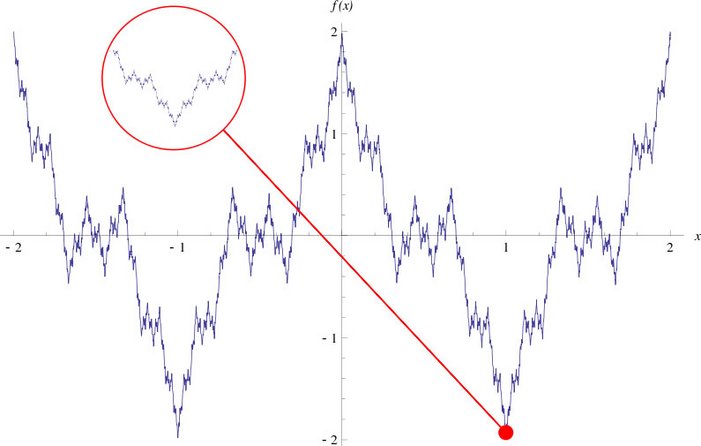
Real functions are discussed, some of which are far from being differentiable.
Examples:
a) Continuous, nowhere differentiable functions, linked to the names Weierstrass, Tagaki, Knopp, Wunderlich,
b) Riemann's famous function, which is differentiable exactly at certain rational points,
c) Singular functions (i.e. (i.e. continuous, monotonically increasing functions that have the derivative zero almost everywhere), associated with the names Cantor, Minkowski, de Rham.
The choice of functions is motivated by two facts:
1) Their irregularity, which is difficult to grasp graphically, has fascinated mathematicians for more than a hundred years and has given rise to many works on the fine structure of real functions.
2) They all satisfy a system of simple functional equations and, on the other hand, can be characterized as a unique solution of this system.
Surprises - from amazement to understanding
Prof. Dr. Wilfried Herget, University of Halle-Wittenberg
Amazement at the unexpected, the surprising, the memorable: this arouses attention, interest, triggers curious questioning and targeted exploration right up to the clarifying resolution of the original tension - an excellent anchor for the joy of questioning and research and for sustainable learning. Numerous examples for the classroom will be presented and actively "lived through".
Program
| 09.30 - 09.45 | Welcome |
| 09.45 - 10.45 | Irregular functions and functional equations (Prof. Dr. H.-H. Kairies) |
| 10.45 - 11.15 | Coffee break |
| 11.15 - 12.15 | Irregular functions and functional equations (Prof. Dr. H.-H. Kairies) |
| 12.15 - 13.30 | Lunch break |
| 13.30 - 14.30 | Surprises - From amazement to understanding (Prof. Dr. W. Herget) |
| 14.30 - 15.00 | Coffee break |
| 15.00 - 16.00 | Surprises - From amazement to understanding (Prof. Dr. W. Herget) |
| 16.00 - 16.30 | Discussion and closing remarks |
Registration and material download
User registration
Please enter the access data provided on the teacher training course in order to access the materials for this course.
Insert registration field
Topic
Surprising features and other curiosities
Event KBS340107
Place
Institute of Mathematics at Clausthal University of Technology
Erzstraße 1
38678 Clausthal-Zellerfeld
Time
October 1, 2013
9:30 a.m. to 4:30 p.m.
Speakers
Herr Prof. Dr. H.-H. Kairies,
Herr Prof. Dr. Wilfried Herget
Contact
Dr. Henning Behnke
Institute of Mathematics
Erzstraße 1
38678 Clausthal-Zellerfeld, Germany
Phone: +49 5323 72-3183
Fax: +49 5323 72-2304
Email: behnke@math.tu-clausthal.de