Statistics
When playing with a fair dice is known that each of the sides is at the top with probability 1/6. But in practical applications, it is rarely the case that in a random experiment the exact probabilities arise due to physical or other conditions.
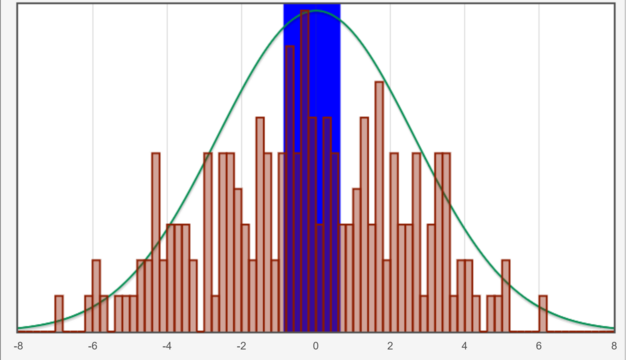
In these cases the statistics comes into play. Its basic idea is to repeat the experiment for which a stochastic description is searched. After sufficiently high number of repeats it is hoped that the result of this sample is representative for the nature of the experiment and from the observed sample results about the distribution of the parameter can be obtained.
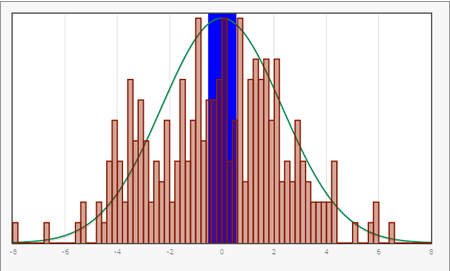
In the descriptive statistics concrete samples are described in terms of characteristics. These mainly include central tendency as the median or the mean value and dispersion measures such as the experimental standard deviation. The number of experiments carried out in this case means sample size.
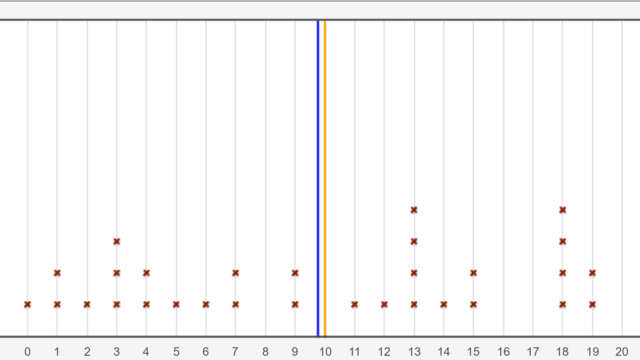
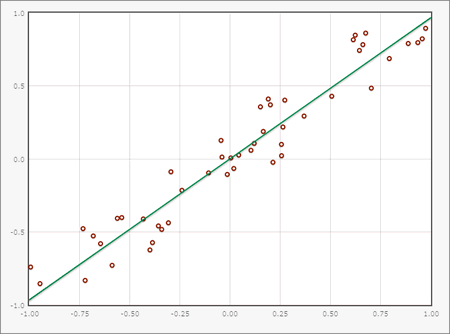
By using the characteristics of the sample actual parameters of each characteristic can be estimated. The strong law of large numbers guarantees that the relative frequency of an event in a sample for increasing sample size converges to the probability of this event, as sought the number of discards fives when throwing a fair die to 1/6. Likewise, the empirical mean converges in a sample to the actual expected value of the distribution; on roling a dice to the average of 3.5. Is only the distribution family of a sample known, in this way, the unknown parameters can be estimated.
However, it is clear that on roling a dice even after very many attempts the relative frequency of the number five, although near 1/6, and the average near 3.5, but can not be guaranteed to be exactly 1/6 and 3.5. Conversely, this means that characteristics or parameters of a distribution can never be estimated exactly by using statistical methods. There is always a degree of uncertainty which has to be be factored in when estimating.
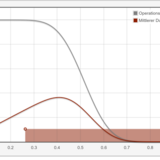
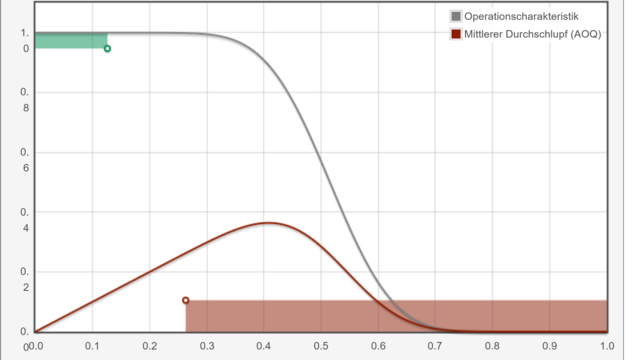
The essential task of inductive statistics is to quantify these uncertainties. The usual methods for these are performing statistical tests and calculating confidence intervals.