
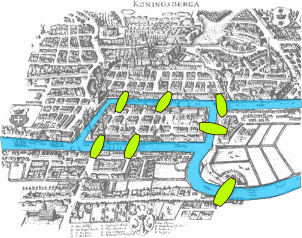
First, an introduction to graphs and their representation possibilities (e.g. by matrices) as well as some well-known graph-theoretical problems (e.g. Königsberg bridge problem, four-color problem) is given.
The lecture "Multi-stage processes" discusses problems in which an initial situation, which can be described by a state vector, is transformed into a subsequent situation with the help of transition matrices. The most important aspects are highlighted using detailed examples.
Many practical problems in everyday life (e.g. route planning) can be modeled and solved with the help of graphs. Some models and optimization methods for solving shortest path problems and round trip problems are presented. Finally, graph coloring problems are considered that have applications in timetabling and sports league planning.
Program
| 09.30 - 09.45 | Welcome |
| 09.45 - 10.30 | Graphs: Introduction and some applications (Prof. Dr. S. Knust) |
| 10.30 - 11.00 | Coffee break |
| 11.00 - 12.15 | Multi-stage processes (Dr. H. Behnke) |
| 12.15 - 13.30 | Lunch break |
| 13.30 - 14.30 | Optimization methods for shortest path problems and round trip problems (Prof. Dr. S. Knust) |
| 14.30 - 15.00 | Coffee break |
| 15.00 - 16.00 | Graph coloring and its applications (Prof. Dr. S. Knust) |
| 16.00 - 16.30 | Discussion and closing remarks |
Topic
Applications of Graphs and Matrices
Course B3.011.MA0
Place
Institute of Mathematics at Clausthal University of Technology
Erzstraße 1
38678 Clausthal-Zellerfeld
Time
March 17, 2010
9:30 a.m. to 4:30 p.m.
Speakers
Frau Prof. Dr. S. Knust,
Herr Dr. H. Behnke
Contact
Dr. Henning Behnke
Institute of Mathematics
Erzstraße 1
38678 Clausthal-Zellerfeld, Germany
Phone: +49 5323 72-3183
Fax: +49 5323 72-2304
Email: behnke@math.tu-clausthal.de