Why are we so often standing in the wrong queue?
If there are several checkouts to choose from, as in a supermarket, people tend to queue at the checkout with the shortest queue in order to minimize their own waiting time.
Problem
However, this strategy obviously does not guarantee that you will be processed more quickly. Since the waiting times of individual customers fluctuate randomly (one has more in their shopping basket, the other less), it can happen that many small orders follow one another in the long queue, while large orders predominate in the shorter queue. In this case, you may have to wait longer in the shorter queue than in the longer queue.
Mathematically, it can be proven that the more irregular the work orders of the individual customers are, the more frequently this situation occurs. (Conversely, if all work orders are roughly the same size, i.e. all customers have roughly the same number of items in their shopping basket, the checkout with the shorter queue will certainly be processed more quickly).
Example
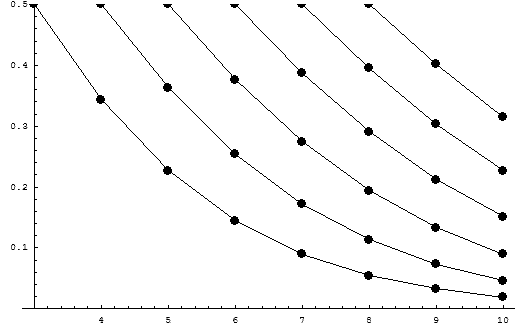
To give a numerical example: Under the prevailing conditions in the supermarket, the probability that a queue consisting of 8 people will be cleared faster than a queue consisting of 5 people is approximately 19%. And even more extreme: the probability that a queue of 10 people will be cleared faster than a queue of only 5 people is still around 9%. These are comparatively high percentages. And this gives the impression of standing in the wrong queue so often.
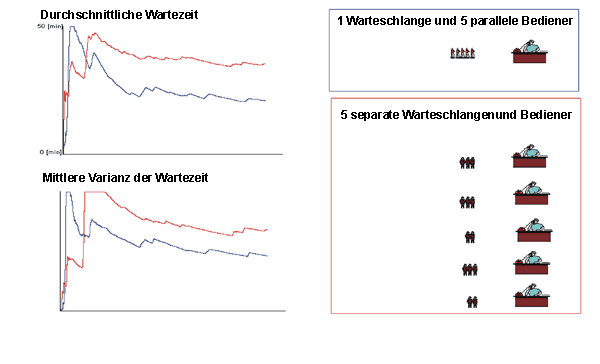
If all customers wait in the same queue, as is the case at airport check-in desks, this impression cannot arise. In addition, by merging the queues, the service counters are also more evenly filled. For example, it is not possible for one counter to be empty while customers are queuing at another. The "American" rule means that the waiting times of customers are not only shortened but also homogenized (i.e. less dispersed), which at the same time achieves greater waiting fairness (see illustration).