"Interpolation" simply means finding a function g from a given class of functions (e.g. polynomials) that runs through given (x, y) points in the plane. This method naturally invites you to approximate a given (generally complicated) function f by a function g from a class of much simpler functions - simply by evaluating the function f at a finite number of points. The "size" of the difference between f and g (the approximation error) depends crucially on the class of functions used for interpolation. We will interpolate with polynomials and so-called radial basis functions and compare the approximation errors with each other.
One tends to think that the approximation error approaches zero if the number of points at which the function f is evaluated approaches infinity. We will show that this is a fallacy. Even "the opposite" is the case: For certain, so-called "universal functions" f, you can find a subsequence of interpolants for every (suitable) function h that converges towards h - and therefore not towards f.
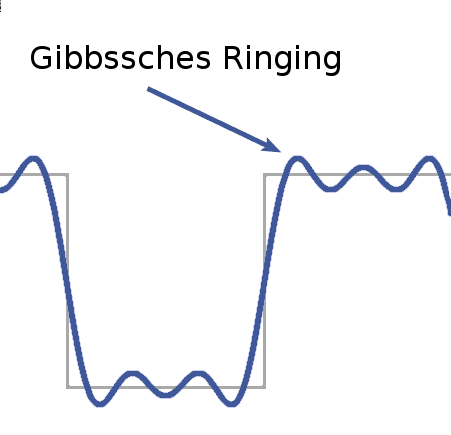
Another way to approximate data or functions is the so-called Fourier analysis - the decomposition of functions into their individual frequencies. We will look at the basic principles and ideas of this theory as well as the many possible applications, e.g. in audio or image analysis.
Finally, we will look at many small mathematical curiosities and bizarre facts from various areas of mathematics that can easily be used in the classroom, such as the question of how two people can share a pizza fairly.
Program
| 09.30 - 09.45 | Welcome |
| 09.45 - 10.45 | From interpolation via approximation to universality (Dr. M. Nieß) |
| 10.45 - 11.15 | Coffee break |
| 11.15 - 12.15 | Introduction to Fourier Analysis I (Dr. F. Philipp) |
| 12.15 - 13.30 | Lunch break |
| 13.30 - 14.30 | Introduction to Fourier Analysis II (Dr. F. Philipp) |
| 14.30 - 15.00 | Coffee break |
| 15.00 - 16.00 | Mathematical curiosities (Dr. M. Nieß) |
| 16.00 - 16.30 | Discussion and closing remarks |
Interpolation, approximation and mathematical curiosities
Topic
Interpolation, approximation, and mathematical curiosities
Course KBS311031
Place
Institute of Mathematics at Clausthal University of Technology
Erzstraße 1
38678 Clausthal-Zellerfeld
Time
March 13, 2013
9:30 a.m. to 4:30 p.m.
Speakers
Herr Dr. M. Nieß,
Herr Dr. F. Philipp
Contact
Dr. Henning Behnke
Institute of Mathematics
Erzstraße 1
38678 Clausthal-Zellerfeld, Germany
Phone: +49 5323 72-3183
Fax: +49 5323 72-2304
Email: behnke@math.tu-clausthal.de