Integration
Integration is the process of calculating indefinite or definite integrals.
The definite integral of a function assigns a numerical value to the function.
This value corresponds to the area which is bounded by the function graph and the x-axis. Here surfaces below the x-axis are counted negatively.
The indefinite integral of a function assigns another functions to it, the function call primitive function. These are characterized by the fact that its first derivative is the function that has been integrated.
The fundamental theorem of calculus states that definite integrals can be calculated by using primitive functions.
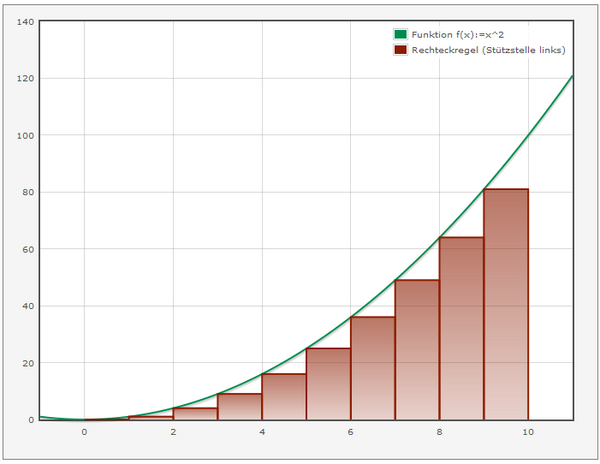
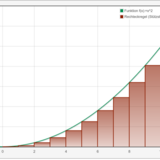
Although one has the impression that the integration is the counterpart of differentiation, integration is much more difficult. To determine derivatives of specific functions, it is sufficient to apply a few defined rules. To integrate elementary functions, however there is no easy and not all cases a concealing algorithm. Here you are much more likely to rely on numerical approximations.